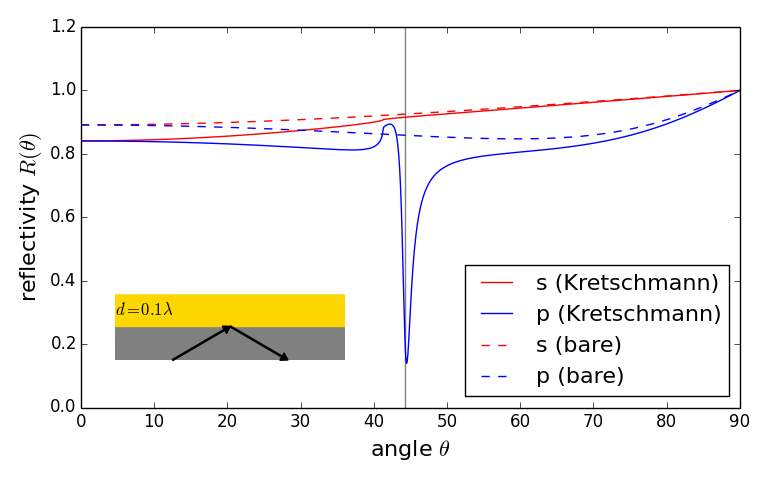
Example: reflectivity vs angle of incidence in Kretschmann configuration (see inset). Metallic layer (epsilon = -9. + 1.3i), dielectric substrate (index = 1.52).

Example: reflectivity vs angle of incidence in
Kretschmann configuration (see inset).
Metallic layer (epsilon = -9. + 1.3i),
dielectric substrate (index = 1.52).
#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
play with multiple layers, using recurrence relation for reflection
amplitudes.
"""
from pylab import *
from matplotlib.patches import Polygon
xsize = 7.5
ysize = xsize*0.5*(sqrt(5)-1)
mysize = 16
tsize = mysize - 4
global n, eps, eps_m, lmbda_v
degree = pi/180.
eps_m = -9. + 1.3*1j # 'typical' metal permittivity
eps = 2.3 # 'typical' dielectric permittivity
n = sqrt(eps)
lmbda_v = 2*pi
def kz_v(theta, n_v = 1.):
"""
wave vector, normal component, in incident medium, normalized to vacuum
wave vector (i.e., vacuum lambda = 2*pi). Here, n_v must be real,
otherwise, the script does not work. Default is vacuum n_v = 1.
"""
return n_v*cos(theta)
def kz_m(q, n_m = n):
"""
wave vector, normal component, in transmitted medium. This may have
complex index n_m. The wave vector q is common to both media,
normalisation such that q = n_v sin(theta)
"""
if size(q) > 1:
kz = zeros_like(q, dtype=complex)
for ii, qi in enumerate(q):
kz[ii] = kz_m(qi, n_m = n_m)
return kz
else:
if imag(n_m) == 0 and n_m < q:
kz = 1j*sqrt(q**2 - n_m**2)
else:
kz = sqrt(n_m**2 - q**2)
return kz
def r_s(theta, n_v = 1., n_m = n):
kz1 = kz_v(theta, n_v = n_v)
kz2 = kz_m(n_v*sin(theta), n_m = n_m)
rs = (kz1 - kz2)/(kz1 + kz2)
return rs
def r_p(theta, n_v = 1., n_m = n):
pz1 = kz_v(theta, n_v = n_v)/n_v**2
pz2 = kz_m(n_v*sin(theta), n_m = n_m)/n_m**2
rp = (pz1 - pz2)/(pz1 + pz2)
return rp
def r_s12(q, eps1, eps2):
kz1 = kz_m(q, n_m = sqrt(eps1))
kz2 = kz_m(q, n_m = sqrt(eps2))
rs = (kz1 - kz2)/(kz1 + kz2)
return rs
def r_p12(q, eps1, eps2):
pz1 = kz_m(q, n_m = sqrt(eps1))/eps1
pz2 = kz_m(q, n_m = sqrt(eps2))/eps2
rp = (pz1 - pz2)/(pz1 + pz2)
return rp
def r_12(q, eps1, eps2, polar):
if (polar == 's') | (polar == 'TE'):
return r_s12(q, eps1, eps2)
elif (polar == 'p') | (polar == 'TM'):
return r_p12(q, eps1, eps2)
else:
print('un-known polarisation, sorry.')
return zeros_like(q)
# reflection coefficients for layered structure
# structure defined by list of pairs (epsilon, thickness * omega/c)
# top (vacuum) and bottom (substrate) layers have no thickness
#
def r_layer(theta, structure = [(1.,), (eps,)], polar = 's', lmbda_v = lmbda_v, Q_verbose = False):
if size(structure) < 2:
print('no well-defined interface(s).')
return zeros_like(theta)
else:
eps_v = structure[0][0] # dielectric constant of vacuum (top medium)
q = sqrt(eps_v)*sin(theta) # theta = angle of incidence in vacuum (top medium)
layer = size(structure) - 2
# initialize reflection amplitude from the bottom
eps_subst = structure[layer+1][0]
eps_layer = structure[layer][0]
R = r_12(q, eps_layer, eps_subst, polar)
if Q_verbose:
if size(R) == 1:
print('%i|%i: R = %3.3g' %(layer, layer+1, abs(R)**2))
else:
for ii, ang in enumerate(theta):
print('theta = %3.2g deg, %i|%i: R = %3.3g'
%(ang/degree, layer, layer+1, abs(R[ii])**2))
while layer > 0:
# add one layer
eps_layer = structure[layer][0]
thick = structure[layer][1]
kz = kz_m(q, n_m = sqrt(eps_layer))
eps_top = structure[layer-1][0]
r = r_12(q, eps_top, eps_layer, polar)
propagate = exp(2j*kz*thick*2*pi/lmbda_v)
R = (r + R * propagate)/(1 + r * R * propagate)
if Q_verbose:
if size(R) == 1:
# print('%i|%i: FP = %3.4g' %(layer-1, layer, abs(1 + r * R * propagate)**2))
print('%i|%i: R = %3.4g' %(layer-1, layer, abs(r)**2))
else:
for ii, ang in enumerate(theta):
# print('theta = %3.2g deg, %i|%i: FP = %3.4g'
# %(ang/degree, layer-1, layer, abs(1 + r[ii] * R[ii] * propagate[ii])**2))
print('theta = %3.2g deg, %i|%i: R = %3.3g'
%(ang/degree, layer-1, layer, abs(r[ii])**2))
layer -= 1
return R
def plot_ellipse(theta, ratio = 1.):
global n, eps
"""
compute polarisation ellipse of incident field, the ratio gives the
ratio between s- and p-polarisation. Coordinate axes: x-axis points
in q direction (parallel to p-polarisation), y-axis along s-polarisation
"""
Ap = -1.
As = 1j*ratio*abs(Ap)
Ax, Ay = Ap, As # vector amplitude
def trace_ellipse(A = (Ax, Ay)):
"""
trace ellipse of polarised light, phi is arbitrary phase that is scanned
"""
nb_phi = 64
phi = linspace(0., 2.*pi, nb_phi)
Ex, Ey = A[0]*exp(1j*phi), A[1]*exp(1j*phi)
return real(Ex), real(Ey)
#
# plot polarisation ellipse for incident/reflected field
color_i, color_r = 'gray', 'b'
x, y = trace_ellipse()
figure(1, figsize = (xsize, xsize), tight_layout = True)
plot( x, y, '-', c = color_i, lw = 1. )
Atot = 1. # sqrt(0.5)*sqrt(abs(Ax)**2 + abs(Ay)**2)
# add labels for `directions' of principal polarisations
text( 0., 1.1*Atot, 's', size = mysize )
text( 1.1*Atot, 0., 'p', size = mysize )
#
# for reflected field
Rp = -r_p(theta)*Ap # minus sign because reference polarisation differs
Rs = r_s(theta)*As
Rx, Ry = Rp, Rs
print('|refl|^2 / |in|^2 = %4.4g'
%((abs(Rx)**2 + abs(Ry)**2) / (abs(Ax)**2 + abs(Ay)**2)))
x, y = trace_ellipse((Rx, Ry))
plot( x, y, lw = 2., label = r'$%3.0f^\circ$' %(theta/degree) )
xlim(-sqrt(2), sqrt(2)); ylim(-sqrt(2), sqrt(2))
legend(loc = 'lower left', fontsize = mysize)
draw()
show(block = False)
return
#
# --- applications start here ---
#
if True:
# simple interface
theta = linspace(0., 90.*degree, 100)
figure(1, figsize = (xsize, ysize), tight_layout = True)
plot( theta/degree, abs(r_s(theta))**2, 'r', label = 's-pol')
plot( theta/degree, abs(r_p(theta))**2, 'b', label = 'p-pol')
xlabel( 'angle $\\theta$', size = mysize )
ylabel( 'intensity $I(\\theta)$', size = mysize )
legend()
figure(2, figsize = (xsize, ysize), tight_layout = True)
plot( theta/degree, angle(r_s(theta))/degree, 'r', label = 's-pol')
plot( theta/degree, angle(r_p(theta))/degree, 'b', label = 'p-pol')
xlabel( 'angle $\\theta$', size = mysize )
ylabel( 'phase [${}^\circ$]', size = mysize )
legend()
if False:
# air spacing between metal and substrate (Otto)
struc = [(eps,), (1.0, 0.2*lmbda_v), (eps_m,)]
figure(1, figsize = (xsize, ysize), tight_layout = True)
# find surface plasmon k-vector
# here (Otto) at vacuum-metal interface
eps_Met = struc[2][0]
eps_Diel = struc[1][0]
eps_Sub = struc[0][0]
k_sp = sqrt(eps_Met*eps_Diel/(eps_Met + eps_Diel))
# translate k_sp into angle, measured with respect to substrate
theta_sp = arcsin(real(k_sp) / sqrt(eps_Sub))
y_max = 1.2
plot( [theta_sp/degree, theta_sp/degree], [0, y_max], c = 'gray' )
# adjust angles for good resolution near the resonance
nb_theta = 200
# theta = linspace(0., 90.*degree, nb_theta)
theta = linspace(0., theta_sp - 5*degree, nb_theta/4)
theta = append(theta, linspace(theta_sp - 5*degree, theta_sp + 5*degree, 2*nb_theta/4))
theta = append(theta, linspace(theta_sp + 5*degree, 90.*degree, nb_theta/4))
plot( theta/degree, abs(r_layer(theta, struc))**2, 'r', label = 's (Otto)')
plot( theta/degree, abs(r_layer(theta, struc, polar = 'p'))**2, 'b', label = 'p (Otto)')
plot( theta/degree, abs(r_s(theta, n_v = sqrt(eps), n_m = 1.))**2, 'r--', label = 's (bare)')
plot( theta/degree, abs(r_p(theta, n_v = sqrt(eps), n_m = 1.))**2, 'b--', label = 'p (bare)')
xlabel( 'angle $\\theta$', size = mysize )
ylabel( 'reflectivity $R(\\theta)$', size = mysize )
ylim(0, y_max)
legend( loc = 'lower right', fontsize = mysize )
# add sketch for layered system
#
l_i, r_i = 0.15, 0.45 # left/right scaled coordinates
b_i, t_i = 0.25, 0.6 # bottom/top
ax = axes([l_i, b_i, r_i - l_i, t_i - b_i])
axis('off')
l_i, r_i = 0, 1
b_i, t_i = 0, 1
for ii, layer in enumerate(struc):
th = 0.2
mat = [(l_i, b_i), (r_i, b_i), (r_i, b_i + th), (l_i, b_i + th)]
if real(layer[0]) > 1:
col = 'gray'
elif real(layer[0]) < 0:
col = 'gold'
else:
col = 'w'
ax.add_patch(Polygon(mat, fc = col, ec = col))
if (ii > 0) & (ii < size(struc)-1): # inner layer, write thickness
d = layer[1]
ax.text( l_i, b_i + 0.5*th, r'$d = %2.2g \lambda$' %(d/(lmbda_v)),
verticalalignment = 'center')
b_i += th
t_i += th
ax.annotate('', (0.5*(l_i + r_i), th), (0.75*l_i + 0.25*r_i, - 0.*th),
arrowprops = dict(facecolor='black', width = 0.8, headwidth = 6))
ax.annotate('', (0.25*l_i + 0.75*r_i, - 0.*th), (0.5*(l_i + r_i), th),
arrowprops = dict(facecolor='black', width = 0.8, headwidth = 6))
if False:
# metallic layer on a substrate (Kretschmann)
nb_theta = 200
theta = linspace(0., 90.*degree, nb_theta)
struc = [(eps,), (eps_m, 0.05*lmbda_v), (1.0,)]
figure(2, figsize = (xsize, ysize), tight_layout = True)
# find surface plasmon k-vector
# here (Kretschmann) at metal-vacuum interface
eps_Diel = struc[2][0]
eps_Met = struc[1][0]
eps_Sub = struc[0][0]
k_sp = sqrt(eps_Met*eps_Diel/(eps_Met + eps_Diel))
# translate k_sp into angle, measured with respect to substrate
theta_sp = arcsin(real(k_sp) / sqrt(eps_Sub))
y_max = 1.2
plot( [theta_sp/degree, theta_sp/degree], [0, y_max], c = 'gray' )
theta = linspace(0., theta_sp - 5*degree, nb_theta/4)
theta = append(theta, linspace(theta_sp - 5*degree, theta_sp + 5*degree, 2*nb_theta/4))
theta = append(theta, linspace(theta_sp + 5*degree, 90.*degree, nb_theta/4))
plot( theta/degree, abs(r_layer(theta, struc))**2, 'r', label = 's (Kretschmann)')
plot( theta/degree, abs(r_layer(theta, struc, polar = 'p'))**2, 'b', label = 'p (Kretschmann)')
plot( theta/degree, abs(r_s(theta, n_v = sqrt(eps), n_m = sqrt(eps_m)))**2, 'r--', label = 's (bare)')
plot( theta/degree, abs(r_p(theta, n_v = sqrt(eps), n_m = sqrt(eps_m)))**2, 'b--', label = 'p (bare)')
xlabel( 'angle $\\theta$', size = mysize )
ylabel( 'reflectivity $R(\\theta)$', size = mysize )
ylim(0, y_max)
legend( loc = 'lower right', fontsize = mysize )
# add sketch for layered system
#
l_i, r_i = 0.15, 0.45 # left/right scaled coordinates
b_i, t_i = 0.25, 0.6 # bottom/top
ax = axes([l_i, b_i, r_i - l_i, t_i - b_i])
axis('off')
l_i, r_i = 0, 1
b_i, t_i = 0, 1
for ii, layer in enumerate(struc):
th = 0.2
mat = [(l_i, b_i), (r_i, b_i), (r_i, b_i + th), (l_i, b_i + th)]
if real(layer[0]) > 1:
col = 'gray'
elif real(layer[0]) < 0:
col = 'gold'
else:
col = 'w'
ax.add_patch(Polygon(mat, fc = col, ec = col))
if (ii > 0) & (ii < size(struc)-1): # inner layer, write thickness
d = layer[1]
ax.text( l_i, b_i + 0.5*th, r'$d = %2.2g \lambda$' %(d/(lmbda_v)),
verticalalignment = 'center')
b_i += th
t_i += th
ax.annotate('', (0.5*(l_i + r_i), th), (0.75*l_i + 0.25*r_i, - 0.*th),
arrowprops = dict(facecolor='black', width = 0.8, headwidth = 6))
ax.annotate('', (0.25*l_i + 0.75*r_i, - 0.*th), (0.5*(l_i + r_i), th),
arrowprops = dict(facecolor='black', width = 0.8, headwidth = 6))
if False:
# waveguide structure, coupled via TIR: error (R > 1) from non-updated
# structure parameter eps_layer (corrected in r_layer)
nb_theta = 200
theta = linspace(30.*degree, 55.*degree, nb_theta)
# theta = linspace(0., theta_sp - 5*degree, nb_theta/4)
struc = [(eps,), (1.0, 0.5*lmbda_v), (1.3*eps + 0.01j, 0.5*lmbda_v), (1.0,)]
fh, md = subplots(1, figsize = (xsize, ysize), tight_layout = True)
sca(md)
plot( theta/degree, abs(r_layer(theta, struc, Q_verbose = False))**2, 'r',
label = 's (waveguide)')
plot( theta/degree, abs(r_layer(theta, struc, polar = 'p'))**2, 'b',
label = 'p (waveguide)')
plot( theta/degree, abs(r_s(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))**2, 'r--',
label = 's (TIR)')
plot( theta/degree, abs(r_p(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))**2, 'b--',
label = 'p (TIR)')
xlabel( 'angle $\\theta$', size = mysize )
ylabel( 'reflectivity $R(\\theta)$', size = mysize )
legend( loc = 'upper left', fontsize = mysize )
# add sketch for layered system
#
l_i, r_i = 0.15, 0.45 # left/right scaled coordinates
b_i, t_i = 0.25, 0.6 # bottom/top
ax = axes([l_i, b_i, r_i - l_i, t_i - b_i])
axis('off')
l_i, r_i = 0, 1
b_i, t_i = 0, 1
for ii, layer in enumerate(struc):
th = 0.2
mat = [(l_i, b_i), (r_i, b_i), (r_i, b_i + th), (l_i, b_i + th)]
if real(layer[0]) > 1:
col = 'gray'
elif real(layer[0]) < 0:
col = 'gold'
else:
col = 'w'
ax.add_patch(Polygon(mat, fc = col, ec = col))
if (ii > 0) & (ii < size(struc)-1): # inner layer, write thickness
d = layer[1]
ax.text( l_i, b_i + 0.33*th, r'$d_{%i} = %2.2g \lambda$' %(ii, d/(lmbda_v)),
verticalalignment = 'center')
if (imag(layer[0]) < 1e-3) & (ii < size(struc)-1) & (abs(layer[0] - 1.) > 1e-3):
ax.text( r_i, b_i + 0.33*th, r'$n_{%i} = %2.2g$' %(ii, sqrt(layer[0])),
ha = 'right', va = 'center')
b_i += th
t_i += th
ax.annotate('', (0.5*(l_i + r_i), th), (0.75*l_i + 0.25*r_i, - 0.*th),
arrowprops = dict(facecolor='black', width = 0.8, headwidth = 6))
ax.annotate('', (0.25*l_i + 0.75*r_i, - 0.*th), (0.5*(l_i + r_i), th),
arrowprops = dict(facecolor='black', width = 0.8, headwidth = 6))
if False:
# waveguide structure, coupled via TIR: error (R > 1) from non-updated
# structure parameter eps_layer (corrected in r_layer)
nb_theta = 450
theta = linspace(40.*degree, 50.*degree, nb_theta)
# theta = linspace(27.*degree, 60.*degree, nb_theta)
# theta = linspace(0., theta_sp - 5*degree, nb_theta/4)
struc = [(eps,), (1.0, 0.5*lmbda_v), (1.3*eps + 0.01j, 0.5*lmbda_v), (1.0,)]
fh, (ph, md) = subplots(2, figsize = (xsize, ysize), tight_layout = True)
# fh, (md) = subplots(1, figsize = (xsize, ysize), tight_layout = True)
sca(md)
plot( theta/degree, abs(r_layer(theta, struc, Q_verbose = False))**2, 'r',
label = 's (waveguide)')
plot( theta/degree, abs(r_layer(theta, struc, polar = 'p'))**2, 'b',
label = 'p (waveguide)')
plot( theta/degree, abs(r_s(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))**2, 'r--',
label = 's (TIR)')
plot( theta/degree, abs(r_p(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))**2, 'b--',
label = 'p (TIR)')
xlabel( 'angle $\\theta$', size = mysize )
ylabel( 'reflectivity $R(\\theta)$', size = mysize )
legend( loc = 'upper right', fontsize = mysize )
sca(ph)
plot( theta/degree, angle(r_layer(theta, struc, Q_verbose = False))/degree, 'r',
label = 's (waveguide)')
plot( theta/degree, angle(r_layer(theta, struc, polar = 'p'))/degree, 'b',
label = 'p (waveguide)')
plot( theta/degree, angle(r_s(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))/degree, 'r--',
label = 's (TIR)')
plot( theta/degree, angle(r_p(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))/degree, 'b--',
label = 'p (TIR)')
xlabel( 'angle $\\theta$', size = mysize )
ylabel( 'phase $\\varphi(\\theta)$', size = mysize )
# legend( loc = 'upper left', fontsize = tsize )
if False:
# one thin layer, used as mirror in Fabry-Perot-like structure
# scan the wavelength
nb_lmbda = 200
freq = linspace(0.5, 2.5, nb_lmbda)
theta = 5.
# model mirror by thin dielectric layer with eps*d = alpha
alpha = 0.25*lmbda_v
d_M = 0.1*lmbda_v
eps_M = alpha/d_M
struc = [(1.,), (eps_M, d_M), (1., )]
RLs = zeros_like(freq)
RLp = zeros_like(freq)
RBs = zeros_like(freq)
RBp = zeros_like(freq)
for ii, f in enumerate(freq):
lmbda = lmbda_v/f
RLs[ii] = abs(r_layer(theta, struc, lmbda_v = lmbda))**2
RLp[ii] = abs(r_layer(theta, struc, 'p', lmbda_v = lmbda))**2
RBs[ii] = abs(r_s(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))**2
RBp[ii] = abs(r_p(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))**2
figure(1, figsize = (xsize, ysize), tight_layout = True)
plot( freq*lmbda_v/(2*pi), RLs, 'r',
label = 's (membrane)')
plot( freq*lmbda_v/(2*pi), RLp, 'b',
label = 'p (membrane)')
plot( freq*lmbda_v/(2*pi), RBs, 'r--',
label = 's (one interf)')
plot( freq*lmbda_v/(2*pi), RBp, 'b--',
label = 'p (one interf)')
text( 0.05, 0.9, r'$\alpha \,=\, %3.4g \,\lambda_0$' %(alpha/lmbda_v),
size = mysize, ha = 'left', transform = ax.transAxes)
text( 0.05, 0.8, r'$d \,=\, %3.4g \,\lambda_0$' %(d_M/lmbda_v),
size = mysize, ha = 'left', transform = ax.transAxes)
xlabel( r'$\mathsf{frequency\ } \omega \lambda_0 / (2\pi c)$', size = mysize )
ylabel( r'$\mathsf{reflectivity\ } R(\omega)$', size = mysize )
legend()
if False:
# sample layered structure
nb_theta = 200
theta = linspace(0., 60.*degree, nb_theta)
d_M = lmbda_v
L = 0.25*lmbda_v
struc = [(1.,), (eps, d_M), (eps_m, L), (1.,)]
plot( theta/degree, abs(r_layer(theta, struc))**2, 'r', label = 's (mirror)')
plot( theta/degree, abs(r_layer(theta, struc, polar = 'p'))**2, 'b', label = 'p (mirror)')
plot( theta/degree, abs(r_s(theta, n_v = sqrt(1), n_m = sqrt(eps)))**2, 'r--', label = 's (bare)')
plot( theta/degree, abs(r_p(theta, n_v = sqrt(1), n_m = sqrt(eps)))**2, 'b--', label = 'p (bare)')
xlabel( 'angle $\\theta$', size = mysize )
ylabel( 'reflectivity $R(\\theta)$', size = mysize )
y_max = 1.
ylim(0, y_max)
legend( loc = 'lower right', fontsize = mysize )
if False:
# Fabry-Perot-like structure, scan the wavelength
nb_lmbda = 200
freq = linspace(0.5, 2.5, nb_lmbda)
theta = 45.*degree
L = 2.5*lmbda_v
# model mirror by thin dielectric layer with eps*d = alpha
alpha = 0.25*lmbda_v
d_M = 0.1*lmbda_v
eps_M = alpha/d_M
struc = [(1.,), (eps_M, d_M), (1., L), (eps_M, d_M), (1.,)]
RLs = zeros_like(freq)
RLp = zeros_like(freq)
RBs = zeros_like(freq)
RBp = zeros_like(freq)
for ii, f in enumerate(freq):
lmbda = lmbda_v/f
RLs[ii] = abs(r_layer(theta, struc, lmbda_v = lmbda))**2
RLp[ii] = abs(r_layer(theta, struc, 'p', lmbda_v = lmbda))**2
RBs[ii] = abs(r_s(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))**2
RBp[ii] = abs(r_p(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))**2
figure(1, figsize = (xsize, ysize), tight_layout = True)
plot( freq*L/(2*pi), RLs, 'r',
label = 's (Fabry-Perot)')
plot( freq*L/(2*pi), RLp, 'b',
label = 'p (Fabry-Perot)')
plot( freq*L/(2*pi), RBs, 'r--',
label = 's (one interf)')
plot( freq*L/(2*pi), RBp, 'b--',
label = 'p (one interf)')
text( 0.05, 0.9, r'$L \,=\, %3.4g \,\lambda$' %(L/lmbda_v),
size = mysize, ha = 'left', transform = ax.transAxes)
xlabel( r'$\mathsf{frequency\ } \omega L / (2\pi c)$', size = mysize )
ylabel( r'$\mathsf{reflectivity\ } R(\omega)$', size = mysize )
legend()
if False:
# random multi-layer structure, scan the wavelength
nb_lmbda = 200
freq = linspace(0.5, 5.5, nb_lmbda)
theta = 50.*degree
nb_layers = 13
# number of layers
random_eps = True # take random dielectric function per layer (>= 1)
if random_eps:
lbel = 'random $\epsilon_i$'
d_tot = 0.25*lmbda_v*nb_layers
d_1 = float(d_tot) / nb_layers
eps_v = 1.
eps_s = eps
struc = [(eps_v,)]
layer = 1
while layer <= nb_layers:
if False:
eps_layer = (1 - ((1.*layer)/(nb_layers+1))**2)*eps_v \
+ ((1.*layer)/(nb_layers+1))**2*eps_s
else:
eps_layer = 0.5 + 1.0*random()
d_layer = float(d_tot) / nb_layers
struc.append((eps_layer, d_layer))
layer += 1
struc.append((eps_s, ))
else:
# random thicknesses of layers
lbel = 'random $\d_i$'
d_tot = 0.
d_1 = 0.1*lmbda_v
eps_v = 1.
eps_s = eps
struc = [(eps_v,)]
layer = 1
while layer <= nb_layers:
eps_layer = eps_s*(layer % 2) + eps_v*((layer-1) % 2)
d_layer = d_1*random()
struc.append((eps_layer, d_layer))
d_tot += d_layer
layer += 1
struc.append((eps_s, ))
RLs = zeros_like(freq)
RLp = zeros_like(freq)
RBs = zeros_like(freq)
RBp = zeros_like(freq)
for ii, f in enumerate(freq):
lmbda = lmbda_v/f
RLs[ii] = abs(r_layer(theta, struc, lmbda_v = lmbda))**2
RLp[ii] = abs(r_layer(theta, struc, 'p', lmbda_v = lmbda))**2
RBs[ii] = abs(r_s(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))**2
RBp[ii] = abs(r_p(theta, n_v = sqrt(struc[0][0]), n_m = sqrt(struc[1][0])))**2
figure(1, figsize = (xsize, ysize), tight_layout = True)
ax = gca()
plot( freq*lmbda_v/(2*pi), RLs, 'r',
label = 's ' + lbel)
plot( freq*lmbda_v/(2*pi), RLp, 'b',
label = 'p ' + lbel)
plot( freq*lmbda_v/(2*pi), RBs, 'r--',
label = 's (one interf)')
plot( freq*lmbda_v/(2*pi), RBp, 'b--',
label = 'p (one interf)')
text( 0.05, 0.9, r'$d_\mathsf{tot} \,=\, %3.4g \,\lambda_0$' %(d_tot/lmbda_v),
size = mysize, ha = 'left', transform = ax.transAxes)
text( 0.05, 0.8, r'$%i\mathsf{\ layers}$' %(nb_layers),
size = mysize, ha = 'left', transform = ax.transAxes)
xlabel( r'$\mathsf{frequency\ } \omega \lambda_0 / (2\pi c)$', size = mysize )
ylabel( r'$\mathsf{reflectivity\ } R(\omega)$', size = mysize )
legend()
if False:
# 'anti-reflection coating' structure with several intermediate layers
nb_theta = 200
theta = linspace(0., 60.*degree, nb_theta)
nb_layers = 65
d_tot = 0.25*lmbda_v
d_1 = float(d_tot) / nb_layers
eps_v = 1.
eps_s = 3*eps
struc = [(eps_v,)]
layer = 1
while layer <= nb_layers:
if False:
eps_layer = (1 - ((1.*layer)/(nb_layers+1))**2)*eps_v \
+ ((1.*layer)/(nb_layers+1))**2*eps_s
else:
eps_layer = (1 - ((1.*layer)/(nb_layers+1)))*eps_v \
+ ((1.*layer)/(nb_layers+1))*eps_s
d_layer = float(d_tot) / nb_layers
struc.append((eps_layer, d_layer))
layer += 1
struc.append((eps_s, ))
figure(1, figsize = (xsize, ysize), tight_layout = True)
ax = gca()
plot( theta/degree, abs(r_layer(theta, struc))**2, 'r',
label = 's (AR)')
plot( theta/degree, abs(r_layer(theta, struc, 'p'))**2, 'b',
label = 'p (AR)')
plot( theta/degree, abs(r_s(theta, n_v = sqrt(eps_v), n_m = sqrt(eps_s)))**2, 'r--',
label = 's (bare)')
plot( theta/degree, abs(r_p(theta, n_v = sqrt(eps_v), n_m = sqrt(eps_s)))**2, 'b--',
label = 'p (bare)')
text( 0.05, 0.9, r'$d \,=\, %3.4g \,\lambda$' %(d_1/lmbda_v),
size = mysize, ha = 'left', transform = ax.transAxes)
if nb_layers > 1:
text( 0.05, 0.8, r'$%i\,\mathsf{layers}$' %(nb_layers),
size = mysize, ha = 'left', transform = ax.transAxes)
xlabel( 'angle $\\theta$', size = mysize )
ylabel( 'reflectivity $R(\\theta)$', size = mysize )
legend()
if False:
# 'anti-reflection coating' structure with several intermediate layers
nb_theta = 200
theta = linspace(0., 60.*degree, nb_theta)
nb_layers = 65
d_tot = 1.0*lmbda_v
d_1 = float(d_tot) / nb_layers
eps_v = 1.
eps_s = 3*eps
struc = [(eps_v,)]
layer = 1
while layer <= nb_layers:
if False:
eps_layer = (1 - ((1.*layer)/(nb_layers+1))**2)*eps_v \
+ ((1.*layer)/(nb_layers+1))**2*eps_s
else:
eps_layer = 1. + random()
d_layer = float(d_tot) / nb_layers
struc.append((eps_layer, d_layer))
layer += 1
struc.append((eps_s, ))
figure(1, figsize = (xsize, ysize), tight_layout = True)
ax = gca()
plot( theta/degree, abs(r_layer(theta, struc))**2, 'r',
label = 's (AR)')
plot( theta/degree, abs(r_layer(theta, struc, 'p'))**2, 'b',
label = 'p (AR)')
plot( theta/degree, abs(r_s(theta, n_v = sqrt(eps_v), n_m = sqrt(eps_s)))**2, 'r--',
label = 's (bare)')
plot( theta/degree, abs(r_p(theta, n_v = sqrt(eps_v), n_m = sqrt(eps_s)))**2, 'b--',
label = 'p (bare)')
text( 0.05, 0.9, r'$d \,=\, %3.4g \,\lambda$' %(d_1/lmbda_v),
size = mysize, ha = 'left', transform = ax.transAxes)
if nb_layers > 1:
text( 0.05, 0.8, r'$%i\,\mathsf{layers}$' %(nb_layers),
size = mysize, ha = 'left', transform = ax.transAxes)
xlabel( 'angle $\\theta$', size = mysize )
ylabel( 'reflectivity $R(\\theta)$', size = mysize )
legend()
show(block = False)