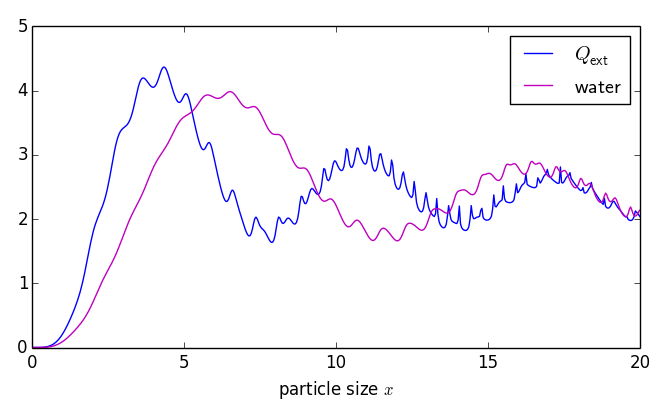
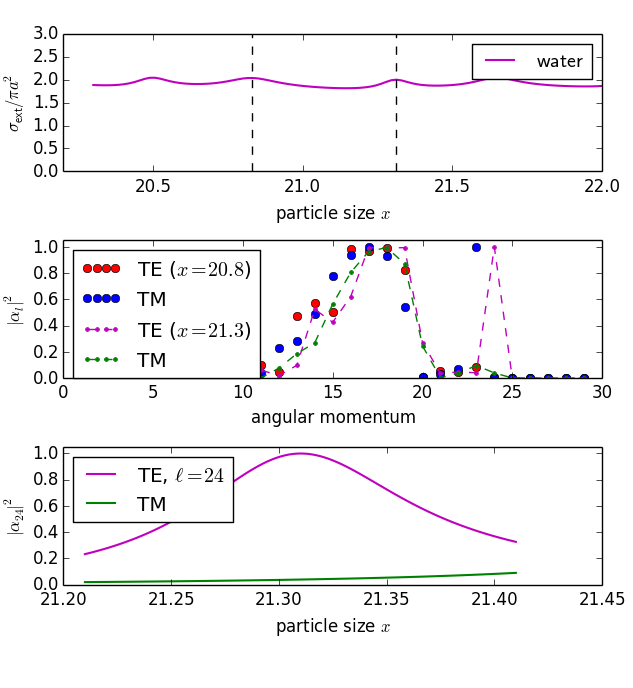
Examples: (left) normalized extinction cross section vs size parameter x = k a. (right) analysis of resonances near l = 24
#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
spherical Bessel functions and Mie solution
"""
from pylab import *
from scipy.special import sph_jn, sph_yn, jv, yv
xsize = 6.5
ysize = xsize*0.5*(sqrt(5)-1)
tsize = 14
def jn(n, x, Q_all = False):
if size(n) > 1 and Q_all:
print('jn: take max of orders n')
nMax = max(n)
out = zeros_like(x)
for ii, xi in enumerate(x):
out[ii] = jn(nMax, xi, Q_all = False)
return out
if size(x) > 1:
out = zeros_like(x)
for ii, xi in enumerate(x):
out[ii] = jn(n, xi, Q_all = False)
return out
else:
out = sph_jn(n, x)[0][-1]
return out # pick from the array only j_n(x)
def hn(n, x, Q_all = False):
if size(n) > 1 and Q_all:
print('hn: take max of orders n')
nMax = max(n)
out = zeros_like(x, dtype=complex)
for ii, xi in enumerate(x):
out[ii] = hn(nMax, xi, Q_all = False)
return out
if size(x) > 1:
out = zeros_like(x, dtype=complex)
for ii, xi in enumerate(x):
out[ii] = hn(n, xi, Q_all = False)
return out
else:
out = sph_jn(n, x)[0][-1] + 1j*sph_yn(n, x)[0][-1]
return out # pick from the array only j_n(x)
def jp_n(n, x, Q_all = False):
"""
related to derivative of Riccati-Bessel function
r = x*j
r' = x*j' + j
divide by x because we work with spherical Bessel
jp = j' + j/x # indeed, n = 0 never appears
"""
if size(n) > 1 and Q_all:
print('jn prime: take max of orders n')
nMax = max(n)
out = zeros_like(x)
for ii, xi in enumerate(x):
out[ii] = jp_n(nMax, xi, Q_all = False)
return out
if size(x) > 1:
out = zeros_like(x)
for ii, xi in enumerate(x):
out[ii] = jp_n(n, xi, Q_all = False)
return out
else:
out = sph_jn(n, x)[1][-1] # pick from the array only jp_n(x)
out += sph_jn(n, x)[0][-1]/x
return out
def hp_n(n, x, Q_all = False):
"""
related to derivative of Riccati-Bessel function
r = x*j
r' = x*j' + j
divide by x because we work with spherical Bessel
jp = j' + j/x # indeed, n = 0 never appears
"""
if size(n) > 1 and Q_all:
print('hn prime: take max of orders n')
nMax = max(n)
out = zeros_like(x)
for ii, xi in enumerate(x):
out[ii] = hp_n(nMax, xi, Q_all = False)
return out
if size(x) > 1:
out = zeros_like(x)
for ii, xi in enumerate(x):
out[ii] = hp_n(n, xi, Q_all = False)
return out
else:
out = sph_jn(n, x)[1][-1] + 1j*sph_yn(n, x)[1][-1] # pick from the array only jp_n(x)
out += (sph_jn(n, x)[0][-1] + 1j*sph_yn(n, x)[0][-1])/x
return out
def ricc_bess(n, x):
return sqrt(0.5*pi*x)*jv(n+0.5, x)
def ricc_bess_h(n, x):
return sqrt(0.5*pi*x)*(jv(n+0.5, x) + 1j*yv(n+0.5, x))
def Mie_denom(ell, x, z, p = 0):
"""
denominator of Mie coefficient, its zeros correspond to scattering resonances
p = 0 is TE polarisation
p = 1 is TM polarisation
"""
n = z/x # relative index of sphere vs exterior
if p == 0:
alph = n*hn(ell,x)*jp_n(ell,z) - hp_n(ell,x)*jn(ell,z)
else: # p == 1
alph = hn(ell,x)*jp_n(ell,z) - n*hp_n(ell,x)*jn(ell,z)
return alph
def Mie_alpha(ell, x, z, p = 0):
if ell == 0:
print('ell = 0 unphysical, return zero.')
return zeros_like(ell)
else:
denom = Mie_denom(ell, x, z, p = p)
n = z/x # relative index of sphere vs exterior
if p == 0:
num = - (n*jn(ell,x)*jp_n(ell,z) - jp_n(ell,x)*jn(ell,z))
else: # p == 1
num = - (jn(ell,x)*jp_n(ell,z) - n*jp_n(ell,x)*jn(ell,z))
return num/denom
def Mie_xs(x, z, Q_lastterm = False, Q_sca = False):
ell_max = int(z + 10) # rough estimate for cutoff of angular
# momentum sum
if not(Q_sca):
Qsum = 0.
for ell in range(1, ell_max):
term = -(2*ell+1)*( real(Mie_alpha(ell, x, z, p = 0)) \
+ real(Mie_alpha(ell, x, z, p = 1)) )
Qsum += term
Qsum *= 2./x**2
if Q_lastterm:
return (Qsum, term)
else:
return Qsum
else:
Qsum = 0.
Qsca = 0.
for ell in range(1, ell_max):
TE_Mie = Mie_alpha(ell, x, z, p = 0)
TM_Mie = Mie_alpha(ell, x, z, p = 1)
term = -(2*ell+1)*( real(TE_Mie) + real(TM_Mie) )
Qsum += term
term_sca = (2*ell+1)*( abs(TE_Mie)**2 + abs(TM_Mie)**2 )
Qsca += term_sca
Qsum *= 2./x**2
Qsca *= 2./x**2
if Q_lastterm:
return ((Qsum, term), (Qsca, term_sca))
else:
return (Qsum, Qsca)
if False:
x_max = 10.
N_x = 64
x = linspace(0.001, x_max, N_x)
if False:
for n in range(5):
figure(1, (xsize, ysize), tight_layout=True)
plot( x, jn(n, x), label = r'$j_{%i}$' %(n) )
xlabel('Mie parameter $x$', size = tsize)
ylabel('spherical Bessel', size = tsize)
legend()
if False:
for n in range(5):
figure(1, (xsize, ysize), tight_layout=True)
plot( x, x*jn(n, x), label = r'$x\, j_{%i}(x)$' %(n) )
plot( x, ricc_bess(n, x), 'x' ) #, label = r'\mathsf{Riccati-Bessel}' )
xlabel('Mie parameter $x$', size = tsize)
ylabel('Mie functions', size = tsize)
legend()
if True:
index = 1.33
x = 8.
z = x*index
ell_max = int(x + 10)
ell_Table = range(1,ell_max)
denom_Table = zeros_like(ell_Table, dtype = complex)
alpha_Table = zeros_like(ell_Table, dtype = complex)
denomM_Table = zeros_like(ell_Table, dtype = complex)
alphaM_Table = zeros_like(ell_Table, dtype = complex)
for ii, ell in enumerate(ell_Table):
denom_Table[ii] = Mie_denom(ell, x, z)
alpha_Table[ii] = Mie_alpha(ell, x, z)
denomM_Table[ii] = Mie_denom(ell, x, z, p = 1)
alphaM_Table[ii] = Mie_alpha(ell, x, z, p = 1)
if False:
figure(2, (xsize, ysize), tight_layout=True)
plot( ell_Table, abs(denom_Table), 'r.')
plot( ell_Table, abs(denomM_Table), 'm.')
xlabel( 'angular momentum')
ylabel( 'Mie denominators' )
if False:
# figure(2, (xsize, ysize), tight_layout=True)
plot( ell_Table, abs(alpha_Table), 'b.--', label = 'TE')
plot( ell_Table, abs(alphaM_Table), 'g.--', label = 'TM')
xlabel( 'angular momentum')
ylabel( 'Mie amplitudes' )
ylim(0, 2)
legend()
if False:
index = 1.33
x_max = 20.
N_x = 200
x = linspace(0.1, x_max, N_x)
Mie_ext = zeros_like(x)
print('compute Mie cross section: will take some time ...')
for ii, xi in enumerate(x):
if ii % 10:
print ii,
Mie_ext[ii] = Mie_xs( xi, xi*index )
figure(3, (xsize, ysize), tight_layout=True)
plot( x, Mie_ext, 'm', label = r'$\mathsf{water}$' )
xlabel('particle size $x$')
ylim(0, 3)
legend()
if True:
index = 1.33
N_x = 100
x = linspace(20.3, 22., N_x)
fh = subplot(3,1,1)
try:
plot( x, Mie_ext, 'm', lw = 1.5, label = r'$\mathsf{water}$' )
except NameError:
Mie_ext = zeros_like(x)
for ii, xi in enumerate(x):
Mie_ext[ii] = Mie_xs( xi, xi*index )
plot( x, Mie_ext, 'm', lw = 1.5, label = r'$\mathsf{water}$' )
xlabel('particle size $x$')
ylabel(r'$\sigma_{\sf ext} / \pi a^2$')
ylim(0, 3)
legend()
fh.set_figsize = (xsize, ysize)
# xi = 20.5
xi = 20.83
fh.plot([xi, xi], [0, 3], 'k--')
ell_max = 30
ell_Table = range(1, ell_max)
Mie_den = zeros_like(ell_Table, dtype = complex)
Mie_denM = zeros_like(ell_Table, dtype = complex)
for ii, ell in enumerate(ell_Table):
Mie_den[ii] = Mie_alpha( ell, xi, xi*index, p = 0 )
Mie_denM[ii] = Mie_alpha( ell, xi, xi*index, p = 1 )
subplot(3,1,2)
plot( ell_Table, abs(Mie_den)**2, 'ro', label = 'TE ($x = %2.3g$)' %(xi))
plot( ell_Table, abs(Mie_denM)**2, 'bo', label = 'TM')
xlabel('angular momentum')
ylabel(r'$|\alpha_l|^2$')
ylim(0., 1.05)
legend()
# xi = 20.83
xi = 21.31
fh.plot([xi, xi], [0, 3], 'k--')
ell_max = 30
ell_Table = range(1, ell_max)
Mie_den = zeros_like(ell_Table, dtype = complex)
Mie_denM = zeros_like(ell_Table, dtype = complex)
for ii, ell in enumerate(ell_Table):
Mie_den[ii] = Mie_alpha( ell, xi, xi*index, p = 0 )
Mie_denM[ii] = Mie_alpha( ell, xi, xi*index, p = 1 )
subplot(3,1,2)
plot( ell_Table, abs(Mie_den)**2, 'm.--', label = 'TE ($x = %2.3g$)' %(xi))
plot( ell_Table, abs(Mie_denM)**2, 'g.--', label = 'TM')
legend(loc='upper left')
if True:
ell = 24
x_zoom = linspace(xi-0.1, xi+0.1, N_x)
Mie_coeff = zeros_like(x_zoom, dtype = complex)
Mie_coeffM = zeros_like(x_zoom, dtype = complex)
for ii, xj in enumerate(x_zoom):
Mie_coeff[ii] = Mie_alpha( ell, xj, xj*index, p = 0 )
Mie_coeffM[ii] = Mie_alpha( ell, xj, xj*index, p = 1 )
subplot(3,1,3)
plot( x_zoom, abs(Mie_coeff)**2, 'm', lw = 1.5, label = r'TE, $\ell = %i$' %(ell))
plot( x_zoom, abs(Mie_coeffM)**2, 'g', lw = 1.5, label = r'TM')
xlabel('particle size $x$')
ylabel(r'$|\alpha_{%i}|^2$' %(ell))
ylim(0., 1.05)
legend(loc='upper left')
if True:
x_inner = linspace(0.1, xi, N_x)
figure(3)
y_data = jn(ell, index*x_inner)*abs(Mie_alpha(ell, xi, xi*index, p = 0))
plot( x_inner, y_data, label = r'$\ell = %i$' %(ell) )
plot( [xi, xi], [min(y_data), max(y_data)], 'k-' )
ell_list = [ell-2, ell-1, ell+1, ell+2]
for m in ell_list:
y_data = jn(m, index*x_inner)*abs(Mie_alpha(m, xi, xi*index, p = 0))
plot( x_inner, y_data, '--', label = r'$\ell = %i$' %(m) )
xlabel('position $k r$')
ylabel('mode function $j_{%i}( n k r )$' %(ell))
legend(loc = 'upper left')
show(block=False)


Examples: (left) normalized extinction cross section vs
size parameter x = k a.
(right) analysis of resonances near l = 24