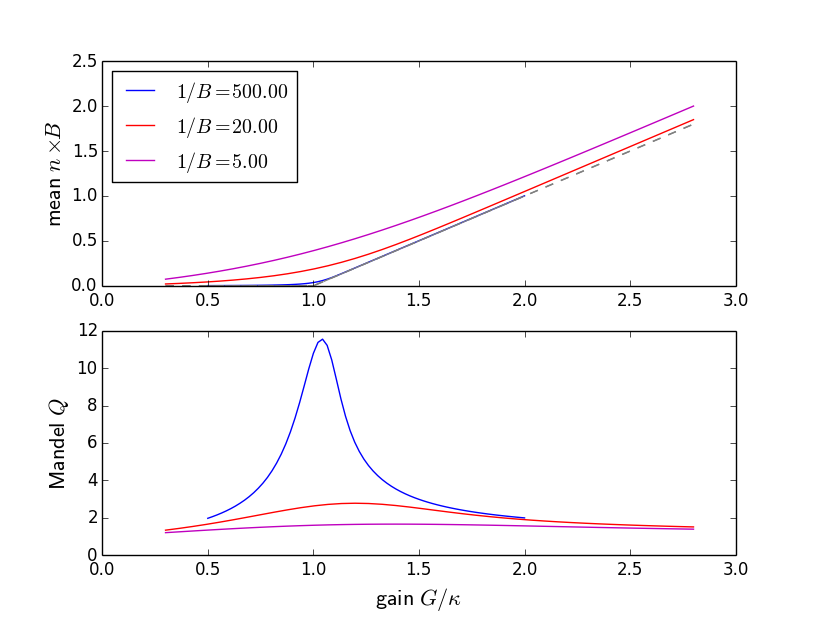
Results of Scully-Lamb laser theory: mean photon number (top) and Mandel parameter (bottom).
#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
Scully-Lamb laser theory: photon statistics from recurrence relation
p_{n+1} = (G/kappa)/(1 + B*n) * p_{n}
max probability at B n_* = G/kappa - 1
taken as starting point (if > 0) for the recurrence relation
"""
print('Scully-Lamb laser theory -- photon statistics')
kappa = 1.
G = 1.1 # small signal amplification
B = 0.1 # inverse of saturation photon number
log_eps = -10. # termination when log p_n < log_eps
def nMax(G = G, B = B, kappa = 1.):
return max(0, (G/kappa - 1.)/B)
def photon_stat(G = G, B = B, kappa = 1., log_eps = log_eps,
Q_plot = False):
n_Star = int(nMax(G/kappa, B))
logp_Star = 0. # arbitrary starting value for log of p_{nStar}
n_List = [n_Star]
logp_List = [logp_Star]
if n_Star > 0:
# backward loop
logp_k = logp_Star
for k in range(n_Star-1, -1, -1):
logp_k = log((1 + k*B)/(G/kappa)) + logp_k # backward recurrence
logp_List.insert(0, logp_k) # prepend probability
n_List.insert(0, k) # prepend photon number to list
# forward loop
logp_k = logp_Star
k = n_Star
while logp_k > log_eps:
logp_k = log((G/kappa)/(1 + k*B)) + logp_k
k += 1
logp_List.append(logp_k) # append probability
n_List.append(k) # append photon number to list
if Q_plot:
print('... photon statistics terminates at n = %i.' %(k))
# normalize by computing the sum (and average n and variance)
p_List = exp(array(logp_List))
n_List = array(n_List)
norm = sum(p_List)
ave_n = sum(p_List*n_List) / norm
var_n = sum(p_List*(n_List - ave_n)**2) / norm
Mandel = var_n/ave_n
if Q_plot: # make a plot of the photon statistics
figure('photon statistics', tight_layout = True)
plot( n_List, p_List, '.-', lw = 1.5 )
plot( [n_Star, n_Star], [0, max(p_List)], '--', c = 'gray' )
plot( [ave_n, ave_n], [0, 1.1*max(p_List)], '-', c = 'gray' )
plot( [ave_n - sqrt(var_n), ave_n + sqrt(var_n)],
[max(p_List)/sqrt(e), max(p_List)/sqrt(e)], '-', c = 'gray' )
yscale('log')
show(block = False)
return ave_n, Mandel
B = 0.2
ave_n, Mandel = photon_stat(1.2, B, Q_plot = False)
print('average photon number: %4.4g' %(ave_n))
print('Mandel parameter: %4.4g' %(Mandel))
if 1/B > 200:
nb_G = 70
G_List = linspace(0.5, 2., nb_G)
else:
nb_G = 40
G_List = linspace(0.3, 2.8, nb_G)
ave_List = zeros_like(G_List)
nMax_List = zeros_like(G_List)
Mandel_List = zeros_like(G_List)
for ii, G in enumerate(G_List):
ave_n, Mandel = photon_stat(G/kappa, B)
ave_List[ii] = ave_n
nMax_List[ii] = nMax(G/kappa, B)
Mandel_List[ii] = Mandel
figure(2)
ax = subplot(211)
l, = plot( G_List, B*ave_List, label = r'$1/B = %3.2f$' %(1/B) )
plot( G_List, B*nMax_List, '--', c = 'gray')
ylabel(r'$\mathsf{mean}\ n \times B$', size = 16)
legend(loc = 'upper left')
subplot(212, sharex = ax)
plot( G_List, Mandel_List, c = getp(l, 'c') )
ylabel(r'$\mathsf{Mandel}\ Q$', size = 16)
xlabel(r'$\mathsf{gain}\ G / \kappa$', size = 16)
show(block = False)

Results of Scully-Lamb laser theory: mean photon number (top)
and Mandel parameter (bottom).