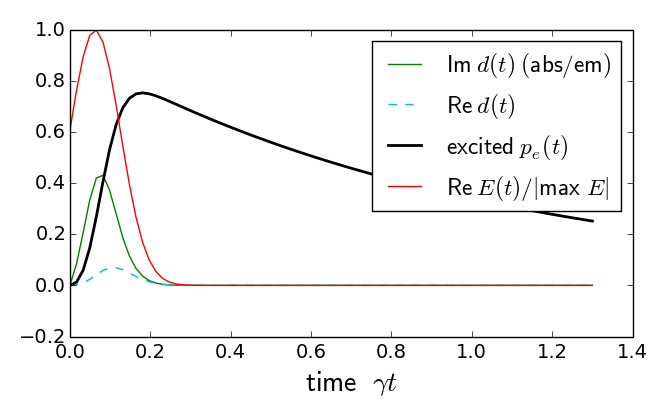
Excitation of a two-level-system with a short pulse: results for the induced dipole
and the excited state population (numerical solution of Bloch equations).
#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
QOI, WS 19/20
-- solve Bloch equations for a two-level system
-- with and without the resonance approximation (also known as
'rotating wave approximation' RWA) and for a
complex Rabi frequency Omega(t), that gives a pulse (envelope)
-- playing with some pictures in the Bloch sphere
(only 2D projections, nothing 3D yet)
"""
from pylab import *
from scipy.integrate import odeint
mysize = 16
tsize = 18
xsize = 6.5
ysize = xsize*0.5*(sqrt(5)-1)
plt.rcParams['figure.figsize'] = (xsize, ysize)
plt.rcParams['figure.autolayout'] = True
plt.rcParams['font.size'] = tsize-4
plt.rcParams['axes.labelsize'] = tsize+2
plt.rcParams['xtick.labelsize'] = tsize-4
plt.rcParams['ytick.labelsize'] = tsize-4
def setParameters(theta0 = 1.0*pi, phi0 = 0., Q_print = False):
# theta0 = pi # (0) is ground (excited) state
"""
set parameters for two-level dynamics (Bloch equations)
cw = True: cw laser
cw = False: pulsed laser (length pulse_tau)
c0 = initial condition for two-level vector (pure state)
t = vector of times 0 < t < tMax where solution is plotted
(default) initial conditions with optional parameters theta0, phi0
"""
global Rabi_f, Laser_f, Atom_f, Gamma_eg, gamma_e, cw, pulse_tau, c0, t, dt, \
Omega, Rabi_env
gamma_e = 1. # decay rate of excited state e
Gamma_eg = (0.0 + 0.5)*gamma_e # dephasing rate, minimum is 0.5*gamma_e
Atom_f = 200.*gamma_e # if the RWA is not applied
Detuning = -0.*gamma_e
Laser_f = Atom_f + Detuning # do not change this line
Rabi_f = 25.0*gamma_e*exp(+0.*pi*1j) # (complex) Rabi frequency
pulsed = True # True = pulsed laser
# pulse area is Rabi_f * sqrt(2*pi) * pulse_tau
pulse_tau = pi/abs(Rabi_f)/sqrt(2*pi)
# pulse_tau = 0.075/gamma_e
# pulse_tau = 1./gamma_e
# interesting time interval
Nb_t = 40
tMax = 3./gamma_e
Nb_t = 80
tMax = 0.3/gamma_e
tMax = max(tMax, 3.*pi/(gamma_e + abs(Rabi_f)))
t, dt = linspace(-0.0*pulse_tau, tMax, Nb_t, retstep = True)
if not(pulsed):
def Omega(t):
return 2.*real(Rabi_f*exp(-1j*Laser_f*t))
def Rabi_env(t):
return Rabi_f*ones_like(t)
else:
def Omega(t):
return 2.*real(Rabi_f*exp(-1j*Laser_f*t))*exp(-0.5*((t - pulse_tau)/pulse_tau)**2)
def Rabi_env(t):
return Rabi_f*exp(-0.5*((t - pulse_tau)/pulse_tau)**2)
# initial conditions, parametrized by angle theta0 on Bloch sphere,
# theta0 = 0 is excited state ('spin up')
# phi0 is relative phase, fixes phase of initial dipole
#
cg0, ce0 = sin(0.5*theta0)*exp(-1j*0.5*phi0), cos(0.5*theta0)*exp(1j*0.5*phi0)
c0 = (cg0, ce0)
if Q_print:
print('|Rabi| = %3.4g gamma' %(abs(Rabi_f)/gamma_e))
if pulsed:
print('laser pulse ~ %3.4g/gamma' %(pulse_tau*gamma_e))
else:
print('cw laser')
print '(c_e(0), c_g(0)) = ',; print(c0[1::-1])
print('time 0 (%3.4g) ... %3.4g / gamma' %(gamma_e*dt, gamma_e*tMax))
return
def RabiH(c, t):
global Rabi_f, Laser_f, Atom_f, Gamma_eg, gamma_e
"""
two-level Hamiltonian applied to vector of amplitudes c = [g(t), e(t)]
written in rotating frame at laser frequency, but not making RWA
i d ce / d t = 0.5*Omega(t)*exp(1j*Laser_f*t)*cg - 0.5*(Laser_f - Atom_f)*ce
i d cg / d t = 0.5*Omega(t)*exp(-1j*Laser_f*t)*ce + 0.5*(Laser_f - Atom_f)*cg
"""
(cg, ce) = c
dotce = -1j*(0.5*Omega(t)*exp(1j*Laser_f*t)*cg - 0.5*(Laser_f - Atom_f)*ce)
dotcg = -1j*(0.5*Omega(t)*exp(-1j*Laser_f*t)*ce + 0.5*(Laser_f - Atom_f)*cg)
return [dotcg, dotce]
def RabiH_rwa(c, t):
global Rabi_f, Laser_f, Atom_f, Gamma_eg, gamma_e
"""
two-level Hamiltonian in resonance approximation (rotating wave, RWA),
in same rotating frame as RabiH, but fast rotating terms dropped
i d ce / d t = 0.5*Rabi_f*cg - 0.5*(Laser_f - Atom_f)*ce
i d cg / d t = 0.5*conj(Rabi_f)*ce + 0.5*(Laser_f - Atom_f)*cg
"""
(cg, ce) = c
dotce = -1j*(0.5*Rabi_env(t)*cg - 0.5*(Laser_f - Atom_f)*ce)
dotcg = -1j*(0.5*conj(Rabi_env(t))*ce + 0.5*(Laser_f - Atom_f)*cg)
return [dotcg, dotce]
"""
The differential equation is solved with the command
odeint(r_Rabi, c0.view(float64), t, full_output = 1)
r_Rabi: command that provides the time derivative, working
with real input and output
c0: the initial condition, complex numbers
t: times where the solution is computed (a vector)
Challenge: 'odeint' works with real-valued functions
the translation from complex to real numbers is done
in Python with the 'view' command. A complex number z
can be converted into a pair of real numbers (with some
floating point precision) with x = z.view(float64).
The reverse is done with z = x.view(complex128).
The following code transforms the function RabiH that
works with complex numbers c = (cg, ce) into a function
that accepts real numbers. Code inspired from
http://stackoverflow.com/questions/19910189/
scipy-odeint-with-complex-initial-values#19921629
"""
def r_Rabi(x, t, *args):
c = x.view(complex128)
dcdt = RabiH(c, t, *args)
return asarray(dcdt, dtype=complex128).view(float64)
def r_Rabi_rwa(x, t, *args):
c = x.view(complex128)
dcdt = RabiH_rwa(c, t, *args)
return asarray(dcdt, dtype=complex128).view(float64)
def BlochL(state, t):
"""
Bloch equations ('superoperator or Liouvillian L')
worked out for complex observables
'state' = [pg, pe, sigma], this is *not* the Bloch vector!
"""
global Rabi_f, Laser_f, Atom_f, Gamma_eg, gamma_e
(pg, pe, sigma) = state
dotsigma = -1j*(Atom_f - Laser_f)*sigma - Gamma_eg*sigma + \
0.5*1j*Omega(t)*exp(1j*Laser_f*t)*(pe - pg)
dotpe = - gamma_e*pe - \
imag(Omega(t)*sigma*exp(-1j*Laser_f*t))
dotpg = - dotpe
return [dotpg, dotpe, dotsigma]
def BlochL_rwa(state, t):
"""
Bloch equations ('superoperator or Liouvillian L')
worked out for complex observables with the RWA
'state' = [pg, pe, sigma], this is *not* the Bloch vector!
"""
global Rabi_f, Laser_f, Atom_f, Gamma_eg, gamma_e
(pg, pe, sigma) = state
dotsigma = -1j*(Atom_f - Laser_f)*sigma - Gamma_eg*sigma + \
0.5*1j*Rabi_env(t)*(pe - pg)
dotpe = - gamma_e*pe - imag(conj(Rabi_env(t))*sigma)
dotpg = - dotpe
return [dotpg, dotpe, dotsigma]
def r_BlochL(x, t, *args):
# mapping of BlochL to function of real parameters
state = x.view(complex128)
dstatedt = BlochL(state, t, *args)
return asarray(dstatedt, dtype=complex128).view(float64)
def r_BlochL_rwa(x, t, *args):
# mapping of BlochL to function of real parameters
state = x.view(complex128)
dstatedt = BlochL_rwa(state, t, *args)
return asarray(dstatedt, dtype=complex128).view(float64)
if True:
# solve equations of motion, pure-state case with Rabi Hamiltonian first
#
print('solve two-level equations')
setParameters(Q_print = True)
# important to signal that c0 has complex entries, otherwise
# the conversion to real pairs does not work
c0 = array(c0, dtype=complex)
sol = odeint(r_Rabi, c0.view(float64), t, full_output = 1)
sol = sol[0].view(complex128)
#
# extract the probability amplitudes from the solution
cg = sol[:,0]
ce = sol[:,1]
rwa = odeint(r_Rabi_rwa, c0.view(float64), t, full_output = 1)
rwa = rwa[0].view(complex128)
#
# extract the probability amplitudes from the solution
cg_rwa = rwa[:,0]
ce_rwa = rwa[:,1]
# take meaningful quantities
pe_t = abs(ce)**2
pg_t = abs(cg)**2
dipole_t = conj(cg)*ce
P = pe_t + pg_t
# take meaningful quantities
pe_rwa = abs(ce_rwa)**2
pg_rwa = abs(cg_rwa)**2
# now solve with dissipation the Bloch equations, using the
# same initial state
(cg0, ce0) = c0
state0 = [abs(cg0)**2, abs(ce0)**2, conj(cg0)*ce0]
#
# again, need to specify that this is a tuple of complex numbers
state0 = array(state0, dtype=complex)
sol = odeint(r_BlochL, state0.view(float64), t, full_output = 1)
sol = sol[0].view(complex128)
#
bg_t = real(sol[:,0])
be_t = real(sol[:,1])
sigma_t = sol[:,2]
# repeat with RWA version of Bloch equations
#
rwa = odeint(r_BlochL_rwa, state0.view(float64), t, full_output = 1)
rwa = rwa[0].view(complex128)
#
bg_rwa = real(rwa[:,0])
be_rwa = real(rwa[:,1])
sigma_rwa = rwa[:,2]
if False:
# test whether numerical solution has real-valued populations
fg = figure('0 reality test')
plot( gamma_e*t, imag(sol[:,0]), 'b', label = r'$\mathsf{Im\ }p_g$' )
plot( gamma_e*t, imag(sol[:,1]), 'r', label = r'$\mathsf{Im\ }p_e$' )
plot( gamma_e*t, imag(rwa[:,0]), 'b+', label = r'$\mathsf{Im\ }p_g$, rwa' )
plot( gamma_e*t, imag(rwa[:,1]), 'r+', label = r'$\mathsf{Im\ }p_e$, rwa' )
xlabel( r'time $\gamma_e t$')
ylabel( r'imag part of populations')
legend()
fg.set_tight_layout(True)
if False:
# check norm of Bloch vector (= 1 for pure states)
fg = figure('1 norm of Bloch vector')
# Hamiltonian case, should be = 1
norm_H = sqrt((pe_t - pg_t)**2 + 4*abs(dipole_t)**2)
plot( gamma_e*t, norm_H, 'k', label = r'$\mathsf{Schr\"odinger}$' )
# norm of Bloch vector (related to purity of state)
norm_B = sqrt((be_t - bg_t)**2 + 4*abs(sigma_t)**2)
plot( gamma_e*t, norm_B, 'b', label = r'$\mathsf{Bloch eqn}$' )
norm_rwa = sqrt((be_rwa - bg_rwa)**2 + 4*abs(sigma_rwa)**2)
plot( gamma_e*t, norm_rwa, 'b+', label = r'$\mathsf{Bloch + rwa}$' )
plot( gamma_e*t, P, 'k.', label = '$\mathsf{total\ } p(t)$, Schr.' )
plot( gamma_e*t, be_t + bg_t, 'b.', label = '$\mathsf{total\ } p(t)$, Bloch' )
xlabel( r'time $\gamma_e t$')
ylabel( r'norm $|{\bf s}(t)|$')
legend()
fg.set_tight_layout(True)
# compare Hamiltonian and Bloch models, not making the RWA
#
if False:
fh = figure('2 Schrödinger vs Bloch')
# plot data from Hamiltonian dynamics
plot( gamma_e*t, pe_t, 'r.--', label = '$p_e(t)$' )
plot( gamma_e*t, pg_t, 'k.--', label = '$p_g(t)$' )
#
# add data from Bloch equations (incl damping)
plot( gamma_e*t, be_t, 'm-', label = '$p_e(t)$ (Bloch)' )
plot( gamma_e*t, bg_t, 'b-', label = '$p_g(t)$ (Bloch)' )
legend(loc = 'upper right')
xlabel(r'$\mathsf{time\ }\, \gamma t$')
ylabel('$\mathsf{populations}$')
fh.set_tight_layout(True)
# compare Hamiltonian and Bloch models, not making the RWA
#
if False:
fh = figure('3 Schrödinger vs Bloch: dipole')
# plot data from Hamiltonian dynamics
plot( gamma_e*t, pe_t, 'r.-', label = '$p_e(t)$' )
plot( gamma_e*t, real(conj(cg)*ce), 'c.-', label = '$\mathsf{Re\ } d(t)$' )
#
# add data from Bloch equations (incl damping)
plot( gamma_e*t, be_t, 'k-', label = '$p_e(t)$ (Bloch)' )
plot( gamma_e*t, real(sigma_t), 'c-', label = '$\mathsf{Re\ } d(t)$ (Bloch)' )
legend(loc = 'upper right')
xlabel(r'$\mathsf{time\ }\, \gamma t$')
fh.set_tight_layout(True)
# compare Bloch to rate equations, for the dipole
#
if False:
fb = figure('6 Bloch vs rate equations: dipole')
# adiabatic elimination of sigma:
# dotsigma = -1j*(Atom_f - Laser_f)*sigma - Gamma_eg*sigma + \
# 0.5*1j*Rabi_env(t)*(pe - pg)
sigma_ad = 0.5*1j*Rabi_env(t)*(be_t - bg_t) / \
(Gamma_eg + 1j*(Atom_f - Laser_f))
plot( gamma_e*t, real(sigma_t), 'c-', label = '$\mathsf{Re\ } d(t)$ (Bloch)' )
plot( gamma_e*t, real(sigma_ad), 'b.', label = 'adiab' )
plot( gamma_e*t, imag(sigma_t), 'm-', label = '$\mathsf{Im\ } d(t)$ (Bloch)' )
plot( gamma_e*t, imag(sigma_ad), 'r.', label = 'adiab' )
legend(loc = 'upper right')
xlabel(r'$\mathsf{time\ }\, \gamma t$')
fb.set_tight_layout(True)
# illustrate RWA for Hamiltonian model
#
if False:
fh = figure('4 Hamiltonian: test RWA')
# plot data from Hamiltonian dynamics
plot( gamma_e*t, pe_t, 'r.-', label = '$p_e(t)$' )
plot( gamma_e*t, pe_rwa, 'r-', label = '$p_e(t)$, rwa' )
# plot( gamma_e*t, pg_t, 'b', label = '$p_g(t)$' )
# plot( gamma_e*t, P, 'k', label = '$\mathsf{total\ } p(t)$' )
plot( gamma_e*t, real(conj(cg)*ce), 'c.-', label = '$\mathsf{Re\ } d(t)$' )
plot( gamma_e*t, real(conj(cg_rwa)*ce_rwa), 'c-', label = '$\mathsf{Re\ } d(t)$, rwa' )
legend(loc = 'upper right')
xlabel(r'$\mathsf{time\ }\, \gamma t$')
fh.set_tight_layout(True)
# illustrate RWA for Bloch model
#
if False:
fh = figure('5 Bloch: test RWA')
#
# data from Bloch equations (incl damping)
plot( gamma_e*t, be_t, 'k', label = '$p_e(t)$ (Bloch)' )
plot( gamma_e*t, real(sigma_t), 'c', label = '$\mathsf{Re\ } d(t)$ (Bloch)' )
plot( gamma_e*t, be_rwa, 'k.', label = '$p_e(t)$ (Bloch), rwa' )
plot( gamma_e*t, real(sigma_rwa), 'c.', label = '$\mathsf{Re\ } d(t)$ (Bloch), rwa' )
legend(loc = 'center right')
xlabel(r'$\mathsf{time\ }\, \gamma t$')
fh.set_tight_layout(True)
# illustrate absorption and stimulated emission
if True:
fh = figure('absorption, stimulated emission')
#
# data from Bloch equations (incl damping)
# dipole is sigma_rwa, plot imaginary part, defined by
# projection onto (negative) complex Rabi frequency
plot( gamma_e*t, - imag(conj(Rabi_env(t))*sigma_rwa)/abs(Rabi_f), 'g', \
label = '$\mathsf{Im\ } d(t) \mathsf{\ (abs/em)}$' )
plot( gamma_e*t, - real(conj(Rabi_env(t))*sigma_rwa)/abs(Rabi_f), 'c--', \
label = '$\mathsf{Re\ } d(t)$' )
plot( gamma_e*t, be_rwa, 'k', lw = 2., label = '$\mathsf{excited\ } p_e(t)$' )
plot( gamma_e*t, -real(Rabi_env(t))/abs(Rabi_f), 'r', label = '$\mathsf{Re\ } E(t)/|\mathsf{max\,} E|$' )
legend(loc = 'upper right')
xlabel(r'$\mathsf{time\ }\, \gamma t$')
fh.set_tight_layout(True)
# plot entropy and purity vs time
#
if False:
fh = figure(5)
# norm_B = sqrt((be_t - bg_t)**2 + 4*abs(sigma_t)**2)
# print('end: norm(B) = %4.4g' %(norm_B[-1]))
# purity = 0.5*(1. + norm_B**2)
# ent = - 0.5*(1. + norm_B)*log(0.5*(1. + norm_B))
# for ii, nrm in enumerate(norm_B):
# if nrm < 1:
# ent[ii] -= 0.5*(1. - nrm)*log(0.5*(1. - nrm))
#
# plot( t, purity, 'm.-', label = 'purity' )
# plot( t, ent, 'b.-', label = 'entropy' )
norm_B = sqrt((be_rwa - bg_rwa)**2 + 4*abs(sigma_rwa)**2)
print('end: norm(B) = %4.4g' %(norm_B[-1]))
purity = 0.5*(1. + norm_B**2)
ent = - 0.5*(1. + norm_B)*log(0.5*(1. + norm_B))
for ii, nrm in enumerate(norm_B):
if nrm < 1:
ent[ii] -= 0.5*(1. - nrm)*log(0.5*(1. - nrm))
plot( gamma_e*t, 0*0.59 + purity, 'm.', label = 'purity (RWA)' )
plot( gamma_e*t, ent, 'b.', label = 'entropy (RWA)' )
xlabel(r'$\mathsf{time\ } \gamma t$')
legend(loc = 'center right')
# plot solutions in Bloch sphere, two projections
#
if False:
fh = figure(4, (2*ysize, ysize))
plot_s1 = False
# make projection of 13 plane (or 23 plane)
nscut = subplot(121)
nscut.set_aspect(1)
nscut.add_patch(Circle((0,0), radius = 1, color = 'lightgray', lw = 2))
nscut.text(-0.9, 0.9, '$|\Omega| =\, %4.4g \,\gamma$' %(abs(Rabi_f)/gamma_e), fontsize = mysize)
nscut.text(-0.9, 0.75, '$\Delta =\, %4.4g \,\gamma$' %((Laser_f - Atom_f)/gamma_e), fontsize = mysize)
nscut.text(-0.08, 0.95, '$|e\\rangle$', fontsize = mysize)
nscut.text(-0.08, -0.95, '$|g\\rangle$', fontsize = mysize)
eqcut = subplot(122)
eqcut.set_aspect(1)
eqcut.add_patch(Circle((0,0), radius = 1, color = 'lightgray', lw = 2))
#
s3 = be_rwa - bg_rwa
s1, s2 = 2.*real(sigma_rwa), -2*imag(sigma_rwa)
if plot_s1:
nscut.plot( s1, s3, 'b.-' )
else:
nscut.plot( s2, s3, 'b.-' )
eqcut.plot( s1, s2, 'm.-' )
sca(nscut)
xlim(-1.1, 1.1); ylim(-1.1, 1.1)
if plot_s1:
xlabel('1 = Re(d)'); ylabel('3')
else:
xlabel('2 = -Im(d)'); ylabel('3')
sca(eqcut)
xlim(-1.1, 1.1); ylim(-1.1, 1.1)
xlabel('Re(d)'); ylabel('Im(d)')
# plot evolution of a 'swarm' of initial conditions
#
if False:
phiT = [0., 0.125*pi, 0.25*pi, 0.375*pi, 0.5*pi]
thetaT = [0.55*pi, 0.5*pi, 0.45*pi]
fh = figure(6, (2*xsize, xsize))
nscut = subplot(121)
nscut.set_aspect(1)
nscut.add_patch(Circle((0,0), radius = 1, color = 'lightgray', lw = 2))
nscut.text(-0.9, 0.9, '$|\Omega| =\, %4.4g \,\gamma$' %(abs(Rabi_f)/gamma_e), fontsize = mysize)
nscut.text(-0.9, 0.75, '$\Delta =\, %4.4g \,\gamma$' %((Laser_f - Atom_f)/gamma_e), fontsize = mysize)
nscut.text(-0.08, 0.95, '$|e\\rangle$', fontsize = mysize)
nscut.text(-0.08, -0.95, '$|g\\rangle$', fontsize = mysize)
eqcut = subplot(122)
eqcut.set_aspect(1)
eqcut.add_patch(Circle((0,0), radius = 1, color = 'lightgray', lw = 2))
for theta0 in thetaT:
for phi0 in phiT:
setParameters(theta0 = theta0, phi0 = phi0)
# theta0 = pi (0) is ground (excited) state
# now solve with dissipation and RWA the Bloch equations, using this
# initial (pure) state
(cg0, ce0) = c0
state0 = [abs(cg0)**2, abs(ce0)**2, conj(cg0)*ce0]
#
# again, need to specify that this is a tuple of complex numbers
state0 = array(state0, dtype=complex)
rwa = odeint(r_BlochL_rwa, state0.view(float64), t, full_output = 1)
rwa = rwa[0].view(complex128)
#
bg_rwa = real(rwa[:,0])
be_rwa = real(rwa[:,1])
sigma_rwa = rwa[:,2]
s3 = be_rwa - bg_rwa
s1, s2 = 2.*real(sigma_rwa), -2*imag(sigma_rwa)
nscut.plot( s1, s3, '.-' )
eqcut.plot( s1, s2, '.-' )
sca(nscut)
xlim(-1.1, 1.1); ylim(-1.1, 1.1)
xlabel('1 = Re(d)'); ylabel('3')
sca(eqcut)
xlim(-1.1, 1.1); ylim(-1.1, 1.1)
xlabel('Re(d)'); ylabel('Im(d)')
show(block=False)

Excitation of a two-level-system with a short pulse:
results for the induced dipole
and the excited state
population (numerical solution of Bloch equations).